How to generate documentation from source code in Linux

Last updated on September 9, 2020 by Dan Nanni

If you are an open-source developer and want to release your project to the public, you may consider publishing source-code documentation for the project. In cases where you are trying to read source code written by others, it will also be helpful if you can get a bird-eye view of the otherwise cryptic source code.

In Linux, doxygen is the de facto standard tool for automatically generating cross-reference documentation from annotated source code. It supports major programming languages including C/C++, Objective-C, C#, PHP, Java and Python. There are more than 350 open-source projects (e.g., Drupal, Gaim, GNU C++ library, KDE) that rely on doxygen for automatic documentation of their source code.

Using doxygen, you can auto-generate API reference documentation of source code, in HTML or LaTex format. You can also visualize class dependency and the relationship between different source files.

In this tutorial, I will explain how to automatically generate documentation from source code in Linux by using doxygen.

Install Doxygen on Linux

For Ubuntu, Debian or Linux Mint:

To install doxygen on Ubuntu, Linux Mint or Debian:

$ sudo apt-get install doxygen
$ sudo apt-get install graphviz

For CentOS, Fedora or RHEL:

To install doxygen on CentOS, Fedora or RHEL:

$ sudo yum install doxygen
$ sudo yum install graphviz

Generate Documentation from Source code with doxygen

To generate documentation of source code, proceed as follows.

First, generate a project-specific doxygen configuration file:

$ doxygen -g my_proj.conf

The above command will generate a template configuration file for a particular project, which you can further customize as described below.

Among others, you can edit the following options in the configuration file.

# document all entities in the project.
EXTRACT_ALL            = YES

# document all static members of a file.
EXTRACT_STATIC         = YES

# specify the root directory that contains the project's source files.
INPUT                  = /home/xmodulo/source

# search sub-directories for all source files.
RECURSIVE              = YES

# include the body of functions and classes in the documentation.
INLINE_SOURCES         = YES

# generate visualization graph by using dot program (part of graphviz package).
HAVE_DOT               = YES

Now go ahead and run doxygen with the configuration file.

$ doxygen my_proj.conf

Documentations are generated in both HTML and Latex formats, and stored in ./html and ./latex directories respectively.

To browse the HTML-formatted documentation, you can use any web browser to open the HTML index file.

$ cd html
$ firefox index.html

doxygen Documentation Screenshots

Here are several screenshots for sample documentations generated by doxygen.

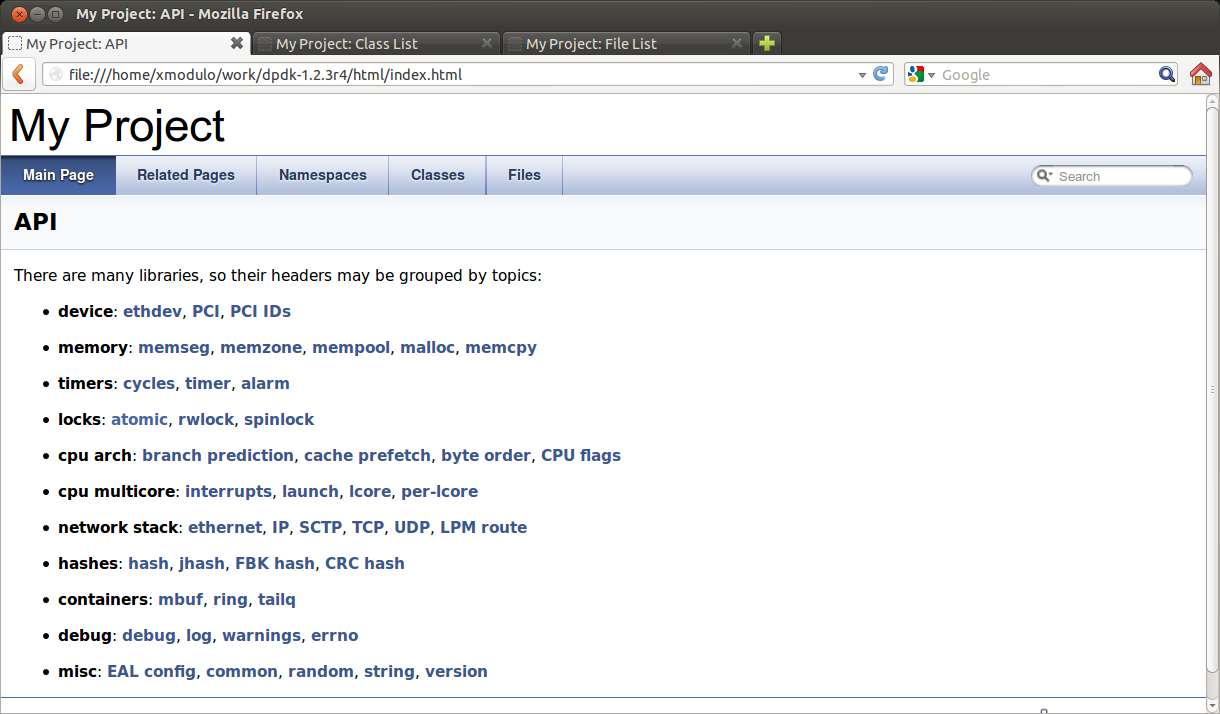
This shows a list of header files that are automatically categorized by topics.

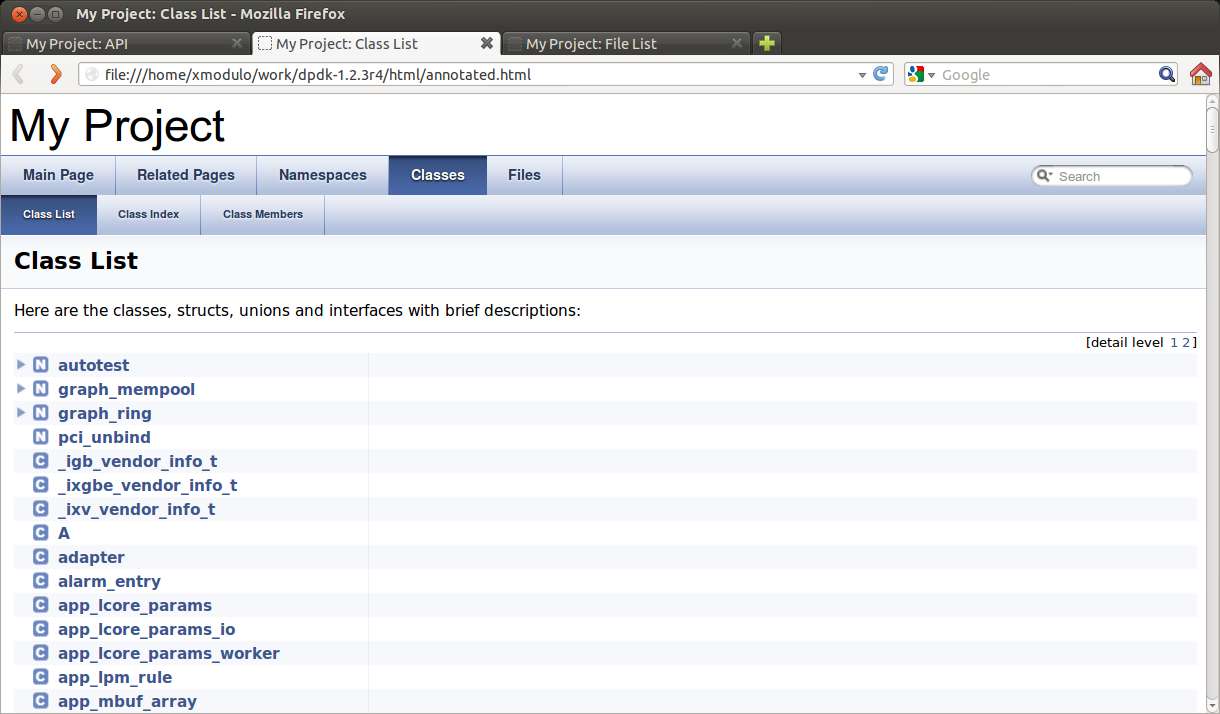
This shows a list of classes, structs, unions and interfaces with descriptions.

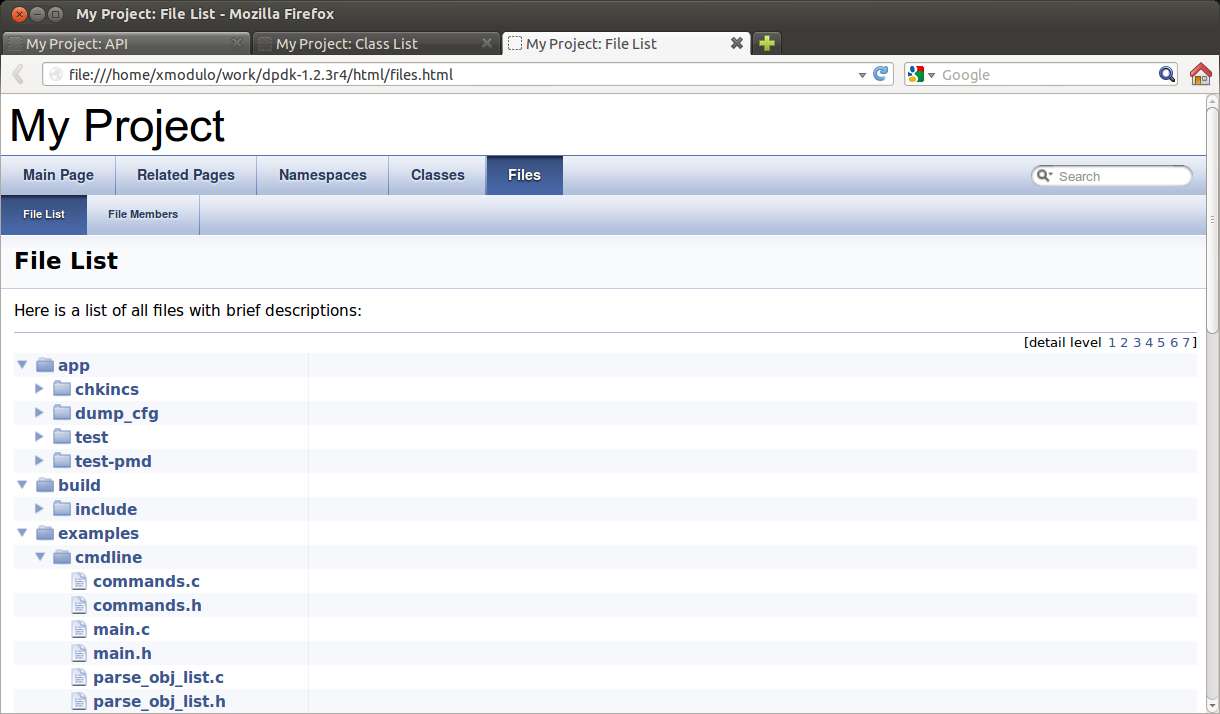
This shows a source code browser listing all source files recursively in sub-directories.

If you click on a particular source file, you will see a page which shows dependency graph for the file, as well as documentation for all defined functions.

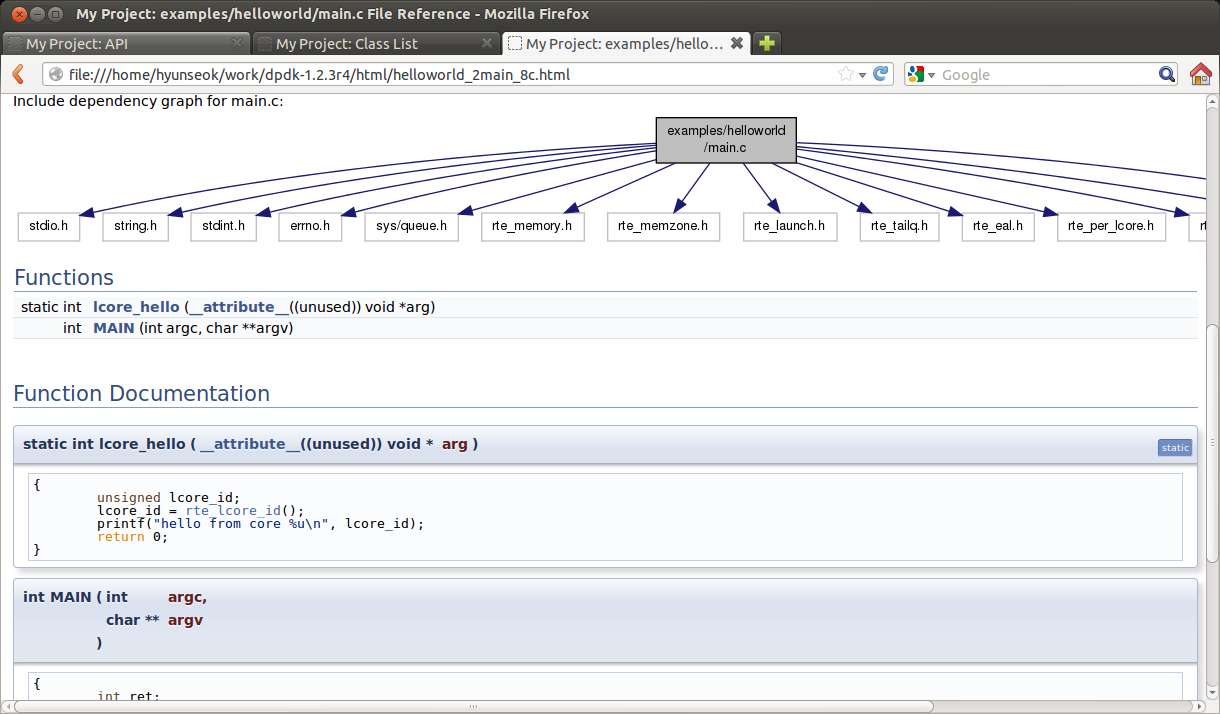
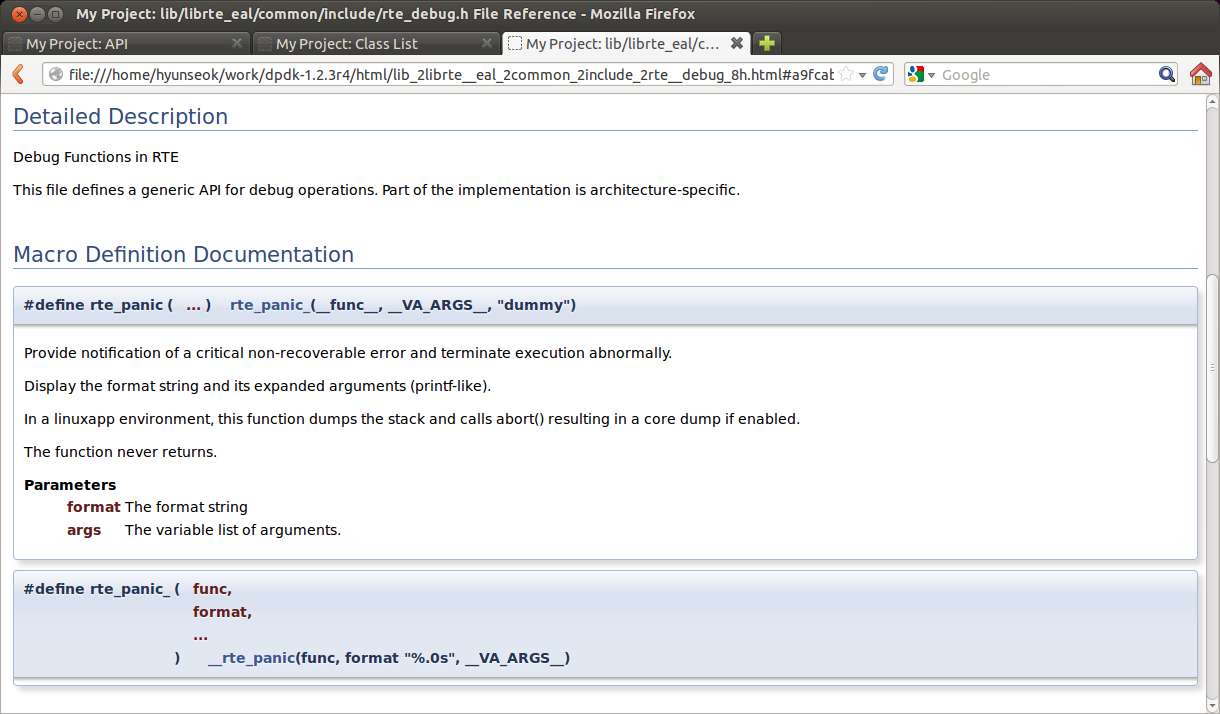
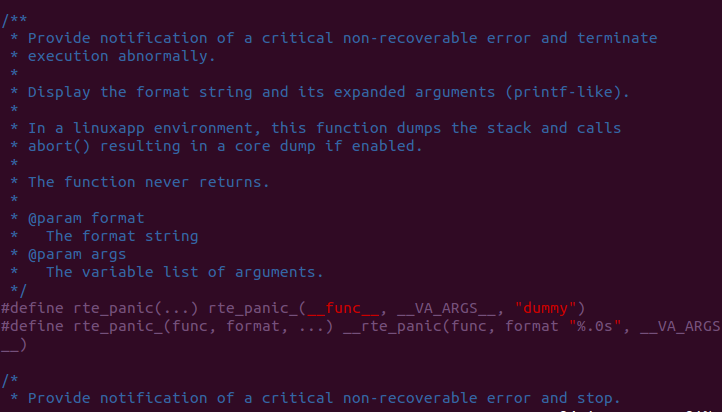
This shows a detailed view of function/macro definitions. Below the figure is shown the actual source code snippet that corresponds to this documented portion.

Support Xmodulo

This website is made possible by minimal ads and your gracious donation via PayPal or credit card

Please note that this article is published by Xmodulo.com under a Creative Commons Attribution-ShareAlike 3.0 Unported License. If you would like to use the whole or any part of this article, you need to cite this web page at Xmodulo.com as the original source.